If you travel a lot by airplane, you have almost surely encountered an overbooked flight. Maybe you were even the person who volunteered to get on a later flight for a $500 or $1,000 voucher. Initially, overbooking seems like an avoidable problem; the airline knows how many seats they have available on each plane after all. So why do they sell more tickets than the maximal seating capacity?
The Cost of No-Shows
The answer lies in the fact that flying with empty seats is costly for airlines. A large fraction of the cost of a flight does not depend on the number of passengers on board. Hence airlines have a large incentive not to leave any seats empty to offset the costs with additional revenue.
Regardless of how many tickets an airline sells for any given flight, there is a high chance that not all ticketed passengers will actually show up for the flight. Some may have changed their travel plans at the last second without canceling, while others may have missed their connection.
How many passengers will be no-shows on any given flight can be estimated using the binomial distribution. The binomial distribution shows us the probability of an event happening exactly X times out of a given number of trials when there are only two possible outcomes. In our case, the passenger either shows up or they don’t, so we can use the binomial distribution to show us how likely it is that X number of seats will be filled when we sell a given number of tickets.
Bionomial Distribution and Empty Seats
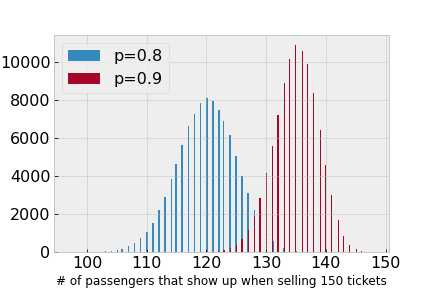
Suppose we have an airplane with 150 seats and let’s say the probability of any passenger showing up for their flight is 80%. To simulate how many passengers will actually be on board when we sell 150 tickets, we have drawn from a binomial distribution 100,000 times and plotted the outcome in the figure below, indicated by the blue graph. As you see, it essentially never happens that all 150 passengers show up if the probability that any given passenger shows up is 80%. If we increase this probability to 90%, it becomes a little bit more likely (as shown on the red graph), but the airline will likely still have a few empty seats.
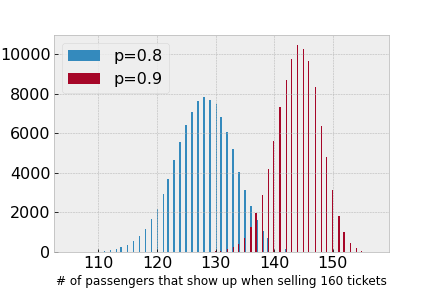
Hence an airline will want to sell more tickets than seats available on each flight. For example, if they sell 160 tickets for 150 seats, they likely will still be able to accommodate everyone on the flight if the probability of any passenger making the flight is 80%. There is also only a small chance of overbooking if 90% of ticketed passengers show up, as illustrated in the graph below.
Optimal Airline Seat Overbooking
The question now is – how many tickets beyond capacity should an airline sell? This will of course depend on a number of factors, such as the capacity of the plane, revenue per passenger, cost of a voucher in case of overbooking, and of course the probability of any given passenger showing up for their flight. As before, let’s assume our plane has 150 seats and that passengers make their flight with a probability 90%. Additionally, suppose revenue per passenger is $250 and the average cost per voucher to the airline is $800.
The airline faces the following trade-off: The more tickets they sell, the more certain they can be that all 150 seats are full and the higher their revenue from ticket sales. However, the more tickets they sell beyond capacity, the higher the probability of an overbooked flight. In this case, voucher payments to customers who need to be bumped will decrease net revenue.
We can plot the expected net revenue for our airline by adapting the Python code written by Cory Simon for our parameter values, as shown in the graph below.
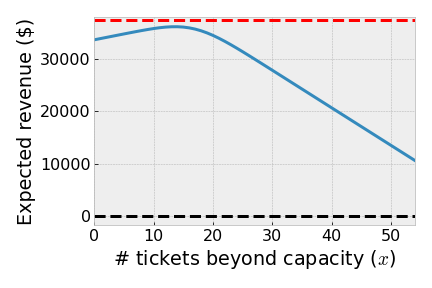
As we see, expected net revenue peaks around 15 tickets beyond capacity. Hence, our airline should sell around 165 tickets for their 150 seat plane.
In summary, an overbooked flight is not a mistake by the airline, but rather revenue-maximizing behavior.
To learn more about probability and its applications in business, become a Buff and take courses in statistics and quantitative analysis!
Eric Hoffmann
Assistant and Pickens Professor of Economics


