Long before Rome was that vast and magnificent empire which occupies a prominent place in the modern public imagination, it was once only one of many fledgling city-states competing for survival and resources on a crowded Italian peninsula. How did this rather unremarkable settlement along the southern banks of the Tiber 2,500 years ago transform itself into the nascent empire that would go on to rule more than 20% of the world’s population, the entirety of the Mediterranean coast, all of modern France, Spain, Belgium, the Middle East, and even the British Isles? What factor allowed this group of people, and not its neighbors, the ability to transcend the endless cycle of local border skirmishes to become arguably Western Europe’s first true hegemon?
These are the questions which encouraged me last summer to read the fantastic book “SPQR” by Mary Beard, whose arguments I will summarize and then augment with my own game theory speculation.
Two Parts Luck, One Part Game Theory
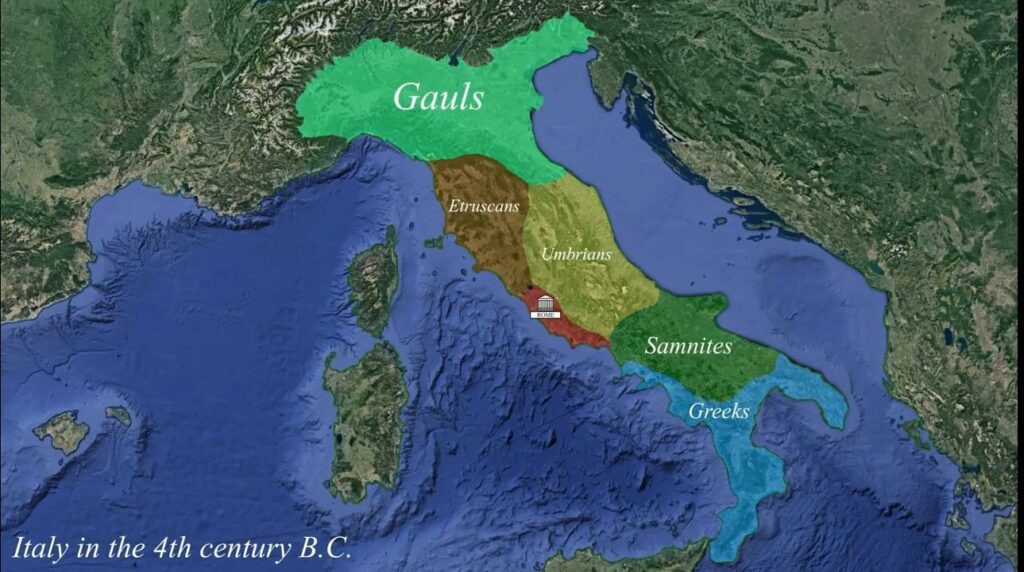
The 4th century BCE was marked by endemic violence on the Italian peninsula. Endless plundering and raiding of one’s neighbors was regarded as a significant source of income. With the Etruscans to the north, the Samnites to the south, and the Umbrians to the east, each of greater territorial size than Rome and the surrounding Latin city-states, what is striking to the modern reader about this period is how average Rome was.
Indeed, as Beard writes:
“First, the Romans were not by nature more belligerent than their neighbors and contemporaries, any more than they were naturally better at building roads and bridges. It is true that Roman culture placed an extraordinarily -for us, uncomfortably- high value on success in fighting.” “Yet”, as she writes, “it would be naïve to imagine that the other peoples in Italy were different.” What, then, allowed Rome to escape this vicious cycle and achieve eventual dominance? Around 350 BCE, Rome experienced its first stroke of luck by finding itself on the winning end of both the Latin War against its immediate neighbors, and shortly thereafter the Samnite Wars against its southern rival.
Its second stroke of luck, however, was not militaristic, but rather strategic. As the victor of these conflicts, Rome was in a position to dictate terms of peace with its conquered foes. But what were these terms to look like? The obvious first guess would be outright territorial acquisition. A Roman-imposed government on its enemies would ostensibly eliminate historical threats, provide increased tax revenue, and increase the amount of soldiers under Roman control. This, however, was not the path that was chosen. As Beard writes:
“There was one obligation that the Romans imposed on all those who came under their control: namely, to provide troops for the Roman armies. In fact, for most of those who were defeated by Rome and forced, or welcomed, into some form of “alliance”, the only long-term obligation seems to have been the provision and upkeep of soldiers. These people were not taken over by Rome in any other way; they had no Roman occupying forces or Roman-imposed government. Why this form of control was chosen is impossible to know. But it is unlikely that any particularly sophisticated, strategic calculation was involved.”
We may speculate that this, as Beard suggests, rather accidental strategy may have provided Rome with significant economies of scale in its costs of expansion. Returns to scale is an economic concept which describes a situation in which the per-unit costs of engaging in an activity actually decrease as more of that activity is done. For example, companies who are able buy input goods in bulk and can do so at a much lower price per-unit, so that average costs of production decrease as production expands.
Similarly, by expanding the amount of manpower under its control while at the same time avoiding all upkeep costs, it is reasonable to expect that the Roman army was able to expand to a size unachievable had it been directly financed by Rome itself. Conquest which leads to expanding manpower and lower costs makes the next conquest that much easier. As Beard writes, “The results may well have been unintended, but they were groundbreaking.”
However, one crucial piece still seems to be missing from the puzzle: Unlike the direct control strategy, allowing conquered territories to retain a large portion of their independence ran the risk of them going back on their agreement once the Romans left town. Why didn’t they? Game theory provides us with an answer.
Self-Interest: The Glue that Holds us All Together
Game theory is a tool which allows us to determine what to expect in situations where the actions taken by one party affect that outcomes of the other. For example, whether or not you decide to purchase a television at Wal-Mart is not a game theoretic situation. Your purchase is too insignificant to affect the market price and subsequently influence my decision. However, how many televisions Sony produces is a game theory situation, as they are large enough to influence the market price and hence the production decisions of other firms. We can visualize situations where parties, commonly known as “players”, are able to impact one another in such ways in diagrams such as the one below:
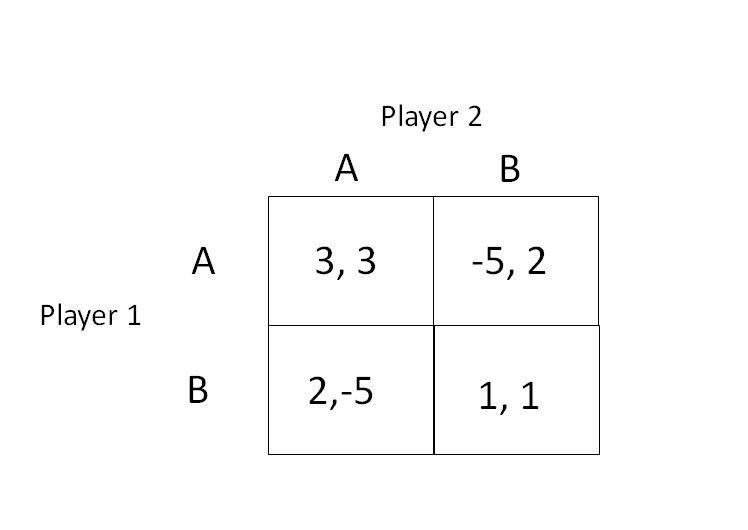
We read this diagram by saying that Player 1 chooses strategy A or B along the left side of the diagram, while Player 2 chooses strategy A or B along the top of the diagram. Any choice of strategies by the two players corresponds to a payoff for both players, so that Player 1 choosing A and Player 2 choosing B corresponds to (-5,2), where Player 1 receives the number on the left (a payoff of negative 5) and player 2 receives the number on the right (a payoff of 2). We can imagine both players indefinitely changing their choice of strategy in order to obtain the highest possible payoff for themselves. A Nash equilibrium occurs when neither player wants to change strategies anymore, providing us with a long-term prediction of the game. Notice that there are two Nash equilibria in this game: Both players choosing strategy A, and both players choosing strategy B. This is because in these scenarios, each player is worse off if they unilaterally change strategies given that their opponent does not change strategies.
The diagram above describes what is known as a typical coordination game in economics. Notice that both players would prefer to coordinate and choose action A so as to both obtain a payoff of 3. However, if for some reason they start at strategy B and are unable to trust the other player to cooperate, then unilaterally deviating to strategy A risks the possibility of getting hit with a huge loss of minus 5. Hence, the inability to trust one another to cooperate may lead both parties to be stuck receiving the suboptimal payoff of 1.
Coordination games describe the situation faced by members of OPEC and other cartels today. Members are asked to cooperate on the strategy of keeping oil production intentionally low so as to decrease the supply and hence increase the price of oil on the world market. However, without sufficient punishments for deviating and individually increasing output, each firm would find it optimal to deviate, ramp up production, and capture more profits. To learn more about cartels, become a Buff and take courses such as Industrial Organization!
They may also describe why Rome’s system of alliances held together so nicely. Imagine Players 1 and 2 as conquered territories, where strategy A represents the option to “break the alliance”, and strategy B represents the option to “stay in the alliance”. As the defeated parties, both players find themselves initially forced into an alliance, playing strategy B, represented in the bottom right of our diagram. Part of the benefit of such an alliance, as Beard writes, was that it “…gave those allies a stake in the Roman enterprise, thanks to the booty and the glory that were shared in the event of victory.”. Hence, maintaining the alliance and sharing the booty gives each of the three parties (Rome and two allies) a payoff of 1 unit of the booty each. Now, if both parties could somehow coordinate to break the alliance and choose strategy A simultaneously, they could avoid having to share amongst each other, securing themselves future payoffs of 3 each.
However, a coordination problem arises: If neither ally can be 100% certain that the other ally will follow through with their promise of breaking the alliance by choosing strategy A, they run the risk of being the lone dissenting ally. In our diagram, this is represented by one of the allies choosing A, but the other remaining with their strategy of B. In this case, the dissenting ally finds itself facing down a tremendous foe: Rome and the other remaining ally. Because this would surely lead to a disastrous outcome, the dissenting ally receives a payoff of -5 in these cases. Hence, possible coordination failure stemming from the uncertainty of the other allies cooperating simultaneously and the disastrous consequences of finding oneself as the only dissenting ally may have been enough to persuade each party to remain in the alliance, and ultimately fuel the economies of scale of Rome’s military expansion.
By 200 BCE, around 150 such treaties had been arranged between Rome and its conquered territories, and the rest, they say, is history. So, if you’re looking to take over the world using game theory, then, as Julius Caesar once famously proclaimed as he crossed the Rubicon river into northern Italy, “Let the die be cast.”.
Dr. Eric Hoffmann
Assistant and Pickens Professor of Economics
References:
- Beard, Mary. SPQR: A History of Ancient Rome. Liveright Publishing Corporation, 2015
- https://www.oxfordreference.com/view/10.1093/oi/authority.20110803100515722


