How do statisticians and scientists come to the conclusions that they do? Are they really uncovering fundamental universal truths with absolute certainty, and if not, why should we trust them? In this essay, we will explore the main tool that experts use to make sense of the world around us: the hypothesis test.
And the wonderful thing is, as complicated as this term may sound, you actually use this tool on a daily basis, whether you realize it or not.
Think On This:
Consider the following scenario: You have been eagerly awaiting the release of a new video game, movie, book, etc., and on the day of the release, you quickly log onto the internet to read the first customer reviews. After sifting through a handful of them, you find that the average review seems to give about 6 out of 10 possible points, or 60%.
What conclusions should you draw?
Naturally, you conclude that this product is not as good as you had hoped. But why is this the correct conclusion? What your brain has implicitly done is what is known as a “hypothesis test”. It turns out, this is same logic that leads scientists to conclude whether or not vaccines are safe for public use, or whether cosmic inflation is a good model of the expansion of the early universe.
Keep this above example in mind, and let’s return to it in a second.
Step 1: Take a Guess, any Guess!
The first step of a hypothesis test is very simple: form a hypothesis. When trying to determine what is most likely true in a given situation, you can make a list of all of the possibilities, and each one of these would be a “hypothesis”. In the example concerning video games above, there are two possibilities, or two hypotheses: The video game is actually good, or the video game is actually bad.
Let us take another example: Suppose that I am presented with a coin, and I am interested to know whether or not it is a fair coin, or one that lands on heads 50% of the time and tails 50% of the time. I may be interested in this if I were making bets based on the outcome of this coin, or if I were a football team hoping to win the opening coin toss. Once again, there are two hypotheses: The coin is fair, or the coin is not fair.
What is key to remember in this step is that it is of absolutely no importance that you guess the “correct” hypothesis. As you will see, if we are clever enough, our strategy will actually be to eliminate hypotheses that are unlikely to be true. This would leave us with only a handful of remaining possibilities, or only one if we are lucky. So go ahead and make an exhaustive list of all of the possibilities, even if you suspect that some of them may be wrong.
Step 2: What would it be like if…
What we want to do here is take one of our hypotheses and ask ourselves what we would expect the world to look like if this hypothesis were actually true. For example, take our video game scenario above, and consider the hypothesis that the game is actually of high quality.
Assuming this to be true, we would probably expect to see reviews on average to be around 80% or above. While it is possible that a good game receives poor reviews, the probability of this occurring is rather low. Alternatively, if we consider the hypothesis that the game is bad, we would expect to see rather low reviews.
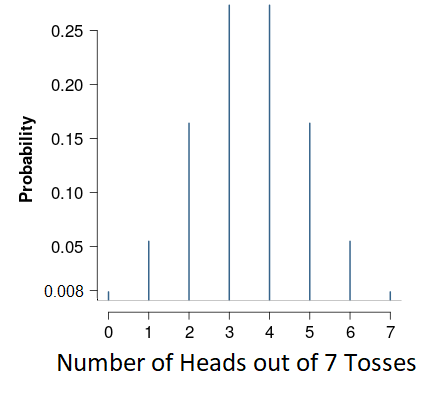
Now let’s take our coin flipping example, and consider the hypothesis that the coin is fair. What would we expect to see if this were actually the case? Here, teasing out the implications of this hypothesis involves some careful probability analysis, which you can learn about in my CIDM 6305 course.
However, allow me to summarize: Given the coin is fair, then if I were to observe seven tosses of the coin, the probability that I see a given amount of those tosses turn up heads is summarized in the table above.
This graph is derived from what is know as a binomial probability distribution. Again, this involves a little knowledge of statistics, but let’s not worry ourselves with this at this point. We now have an idea of what the world would look like if the hypothesis of the coin being fair were true.
Step 3: Process of Elimination
Ok. Last step. What now? Let’s summarize where we’re at. We’re faced with a given scenario, maybe trying to determine if the video game is good or not, or whether a coin is fair. In each scenario, we have a list of possibilities, or hypotheses. Associated with these hypothesis is a prediction of how the world would look like if that hypothesis were true. The last step is then to observe the real world, and check to see if the what we see in the real world is consistent with the implications of the given hypothesis.
Let’s begin with our video game example. Once again, consider the hypothesis that the game is of high quality. If this were true, as we argued above, we would probably expect to see reviews on average to be at least 80%. However, given that we are actually observing reviews on the order of 60%, we are lead to reject the hypothesis that the game is good.
This is because what we observe in the real world (60% reviews) is not consistent with what the world would look like if the game were good (reviews of 80% or above). Notice that I’ve gone through a lot of explaining and formality simply to arrive at the same conclusion that your brain arrives at almost automatically without you even thinking about it. But this is exactly the logic of hypothesis testing, which you likely do multiple times as you go about your day.
Back To The Coin Toss…
Now let’s turn to the coin toss example. Consider the hypothesis that the coin is fair, and suppose that after seven tosses of the coin, you observe zero heads. Looking at our table above, while this outcome is certainly possible, it should only occur about .008% of the time. That is, in 1 – .008 = .992% of the cases, you would observe at least one coin flip turn up heads if the coin were in fact fair.
What we say in this case is that you can reject the hypothesis of the coin being fair with .992% confidence. Equivalently, and in the language of statisticians, you would say that you reject the hypothesis at a “p-value” of .008. See what they did there? They simply reported the .008 instead of the .992 and attached a fancy word called p-value to confuse everybody. Welcome to academia.
Now what if you observed not zero but exactly one of the seven coins tosses turn up heads? Again, this is a possibility, but this only occurs approximately .05% of the time. Statisticians are usually confident in rejecting possibilities which only occur .05% of the time, and so you can confidently reject the hypothesis of a fair coin again as well.
However, we can be a little less confident this time in rejecting compared to having observed zero heads, since the latter occurs even less often, with a probability of .008% compared to .05%.
In Conclusion
As you can see, the idea of hypothesis testing is rather simple: List out all of the possibilities or hypothesis, ask yourself what you would expect to see if any of them were true, and compare that with what you see in the real world. If what you observe in the real world is wildly inconsistent with what that hypothesis would suggest, you can then safely reject that hypothesis.
In this light, rather than confirming or discovering fundamental truths about the universe, the job of the scientist can be seen as rejecting ideas that are not true. Through this careful process of elimination, we become better able to understand how the world around us works.
If you would like to learn more about hypothesis testing, become a Buff and take courses like business statistics or quantitative analysis.
Eric Hoffmann
Associate and Pickens Professor of Economics

