If recent years have taught us anything, it’s that the increase in the availability of information made possible by our almost unfettered interconnectivity and access to data has not been met with a reduction in people’s propensity to congregate around seemingly outlandish ideas. “Extraordinary claims require extraordinary evidence.”, as Carl Sagan once said, and this past decade has given rise to a host of movements and actions in which this criterion seems woefully unfulfilled: The rise of the anti-vaccination movement, the claim that the top echelons of government are being occupied by a race of extraterrestrial lizard people, a resurgence of the idea that the earth is flat, and a conspiracy-fueled storming of the United States Capitol building, to name just a few. This inverse relationship between action and supporting evidence demands explanation.
As easy as it is to laugh at the aforementioned cases (either mockingly or in horror), more benign examples are ubiquitous in economics and society, and it’s very likely that you’ve exhibited such behavior yourself. Consider the following scenario: You are traveling to a conference. With your phone out of power, you lose track of time, and the best you can remember is that the event is slated to begin at 10:30 am. However, as you approach, you find that a group of people are already entering the location at 9:30 am. With the mass of people behaving counter to what you would have done based on your information, you conclude that you are the one who must have been mistaken and decide to enter at 9:30 as well. You are surprised to find out that the event actually does begin at 10:30, and that it was the rest of the crowd that was mistaken.
What has happened here? Are you a proverbial “sheep” for willingly ignoring your own correct information and following the crowd, only to be misled into making the wrong choice by doing so? In their paper “A Theory of Fads, Fashion, Custom, and Cultural Change as Informational Cascades”, Bikhchandani, Hirshleifer, and Welch argue that the opposite is true: Your willingness to follow the crowd was actually rational and justified. The idea is simple. Not only do we obtain information from our own private sources, but we also observe the actions of others and deduce what information they must have had which led them to their behavior. Using basic probability theory, which we cover in my CIDM 6305 course, it turns out that despite your personal belief of a 10:30 start time, which may in fact be correct, observing more and more people entering at 9:30 begins to provide overwhelming evidence that 9:30 is in fact the correct start time, and the rational choice is to then follow suit. This is what we call herd behavior. Herd behavior is a situation in which the information derived from the actions of others becomes disproportionally more reliable than your own private information, even though the latter is correct.
But a subtle and important question remains: Even if we assume that people are more often than not correct in their beliefs, so that the vast majority of people are correctly informed of the 10:30 start time, how is it possible to get a large crowd of people entering at 9:30? That is, how do herds begin? In the following section, I summarize the arguments of Bikhchandani, Hirshleifer, and Welch, and derive the actual probability of a herd forming.
Herd Immunity? Don’t Count on It.
Consider a simple scenario: A group of individuals arrive at the location of the conference one at a time. Each individual has an 80% probability of knowing the correct start time of 10:30, but has a 20% probability of incorrectly believing the start time to be 9:30. Each person’s information is assumed to be equally reliable (that is, my memory is not inherently better than yours at remembering what the correct time is). By working backwards, we will see that a herd can form with the arrival of the third individual. That is, using our definition of herd behavior, if the third individual observes the first two individuals entering the building at 9:30, then even if she correctly believes that the start time is 10:30, it is mathematically justified for her to ignore her own information and assume 9:30 to be the correct start time. We will ignore this slightly more complex calculation and simply concentrate on the probability of the third individual observing the first two entering at 9:30.1
Assume that the first individual has incorrect information, and, being the first to arrive, acts accordingly and enters the building at 9:30. By assumption, this happens 20% of the time. Now the second individual arrives. With 20% probability, she has wrong information as well, and hence individual 3 observing the first two individuals entering at 9:30 based on both having wrong information has a probability of 20% x 20%=4%.
It is also possible that the second individual arrives with correct information of a 10:30 start time, which occurs 80% of the time. However, observing the first individual behaving in a way that can only be explained by a belief that 9:30 is correct, and given that each person’s information is assumed equally reliable from the perspective of the other, then taking both sources of information into account, individual 2’s mathematically correct belief (based on a process known as “Bayesian updating”) is to weigh both 9:30 and 10:30 as equally as likely. Assuming that individual 2 breaks such ties by flipping a coin, then individual 1 and 2 entering the building at 9:30 based on individual 1 receiving incorrect information and individual 2 receiving correct information occurs 20% x 80% x 50%=8% of the time. (Footnote: The 20% comes from individual 1 receiving wrong information, the 80% comes from individual 2 receiving correct information, and the 50% comes from individual 2 breaking the tie and entering at 9:30 with 50% likelihood.)
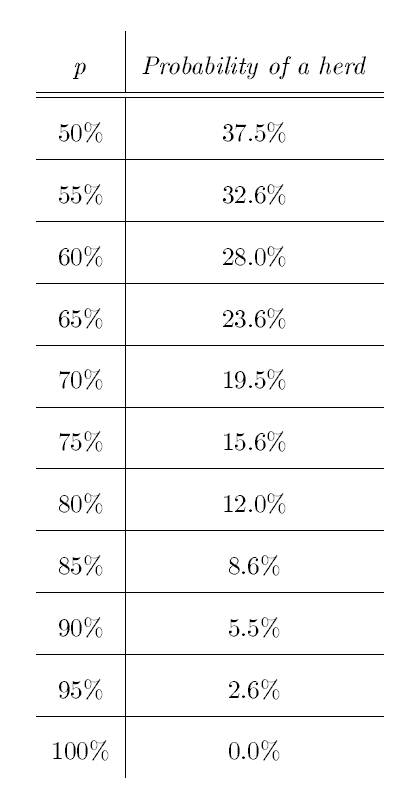
The above two cases exhaust all of the possibilities of how individual 3 could arrive at the location and observe the first two individuals entering the building at 9:30. As explained above, regardless of whether or not individual 3 has correct information, she will calculate that it is more probable than not that the correct start time is 9:30 and act accordingly, and hence a herd will begin. Using our calculations above, we see that even though 80% of individuals have correct information, the probability of a herd formation is still quite high, with a 4%+8%=12% chance. If we replace our 80% probability with p, and our 20% probability with 1-p, we then have a general formula for herd behavior to form, which is given by
(1-p)2 +0.5p(1-p)
Using the above formula, the table below gives the probabilities of herd behavior based on different choices for p, the probability that each individual has of having correct information:
References
Bikhchandani, Sushil, David Hirshleifer, and Ivo Welch. “A theory of fads, fashion, custom, and cultural change as informational cascades.” Journal of Political Economy 100.5 (1992): 992-1026.
Eric Hoffmann
Assistant & Pickens Professor of Economics


