Here’s an interesting little problem that I’m often asked by students: If a company wants to maximize the amount of money it brings in (its “revenue”), shouldn’t it simply produce and sell as much as it possibly can? This is an intuitive first attempt at thinking about this problem: Since total revenue is simply the price of the product multiplied by the amount of product sold, or
Total Revenue = P x Q,
then whatever the price P happens to be, we should just make our quantity sold Q as large as possible. Right? The problem here is that this ignores the complications posed by one of the most important laws in economics: The law of demand. The law of demand states that consumers will be willing to pay a lower and lower price for a product each time more of the product is produced and more is made available to purchase. For example, if there is only one Xbox sitting on the shelf at Walmart, then it can probably fetch a very high price. But if there are hundreds of them sitting on the shelf, then consumers will not be willing to spend so much in order to get one, because they are so widely available.
How does this change our calculation above? We immediately see that simply making Q as large as possible is not the obvious solution anymore. Why? This is because every time we increase the amount sold Q, the price P goes down, and it’s not clear that this new combination will give a higher revenue when you multiply the two terms together. So, where do we go from here?
Elasticity
The concept of the elasticity of demand plays a key role in economic analysis, as it gives us a way of measuring how sensitive price changes are to changes in the amount of output produced. According to the law of demand, we know that prices have to decrease if we produce more output. But will this be a drastic price decrease, or only a small price decrease? It’s not hard to imagine that having such knowledge can help up with out revenue maximization problem above. But how do we calculate elasticity? In principle, this is an easy task, as the elasticity of demand formula is given by
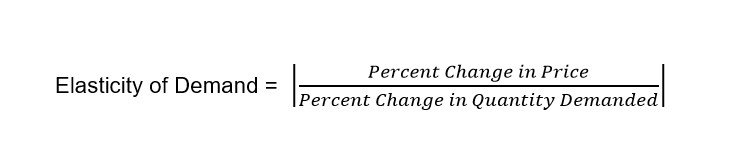
In English, given some increase in quantity Q, we can calculate the percent change of that increase, as well as the percent change of the price the product demands due to that change. By dividing these two terms (and then taking the absolute value of them), we get a sense of how large the price change was relative to how large the quantity change was, in percentage terms.
Solving The Original Problem
The concept of elasticity of demand can help us solve our problem of revenue maximization. How so? Although it goes beyond the scope of this blog post to formally prove this to be the case, it turns out that revenue is maximized when the firm produces that amount of quantity Q so that the elasticity of demand is exactly equal to 1. Let’s take a look at a numerical example and see why this might be the case. Suppose that the price of a good is given by the equation
P=10-Q.
Then we can make the following table:
| Q | P | Total Revenue = PxQ |
| 0 | 10 | 0 |
| 1 | 9 | 9 |
| 2 | 8 | 16 |
| 3 | 7 | 21 |
| 4 | 6 | 24 |
| 5 | 5 | 25 |
| 6 | 4 | 24 |
| 7 | 3 | 21 |
| 8 | 2 | 16 |
| 9 | 1 | 9 |
| 10 | 0 | 0 |
We see from the table above that total revenue is maximized when the firm produces Q=5 units of output. Now let’s make a table comparing output levels to elasticity. Deriving the formula for elasticity takes a little bit of calculus, and you can learn more about this in my Industrial Organization 4301 course. For our purposes, I will simply provide it for you. Given our price equation about, the elasticity of demand given an amount of output Q produced is given by

By The Numbers
If we construct a table, we have the following:
| Q | Elasticity of Demand |
| 0 | 0 |
| 1 | 1/9 |
| 2 | ¼ |
| 3 | 3/7 |
| 4 | 2/3 |
| 5 | 1 |
| 6 | 3/2 |
| 7 | 7/3 |
| 8 | 4 |
| 9 | 9 |
| 10 | undefined |
Notice that our theoretical prediction is absolutely correct: Producing an output of Q=5 units coincides not only with an elasticity of demand of 1, but it also produces the greatest total revenue. The intuition for this can be thought of as follows: As we increase output from 0 to 1, we have a relatively small decrease in prices, as our elasticity of demand is only ¼. That means that we do not incur much of a cost in terms of a reduction in P when we increase Q, and so that PxQ term will continue to increase.
Beyond an elasticity level of 1, however, the gain made in PxQ term by increasing the Q term by one more unit is offset by a more than one decrease in the P term, as is evident by the 3/2 elasticity value as we go from 5 to 6. This means that the PxQ calculation will actually start to decrease as we increase Q beyond this point.
Eric Hoffman


