“CDC observes link between Covid-19 spikes and increased dining out – The findings don’t prove cause and effect, but the statistically significant patterns are in line with previous studies and expert advice.”
“Pfizer says South African variant could significantly reduce protective antibodies”
Over the last few months, we have seen headlines like these on a regular basis. If you have ever taken a statistics course, you may vaguely recognize the words “statistically significant”. Most of us however probably struggle to remember the details. So what does it really mean if something is “statistically significant”?

How much evidence is enough?
To understand what it means for something to be “statistically significant”, we first have to talk a little bit about hypothesis testing and types of errors. As a simple example, suppose you have the hypothesis that the average height of males in Germany is not the same as the average height of males in the United States. This is your research hypothesis that you’d like to prove, which is also called the “alternative hypothesis”. The opposite case, that is, the average height of males in Germany is equal to the average height of males in the United States, is what we’ll call your “null hypothesis”. I know this seems a little bit backwards, but you will see why in a moment. Only one (and exactly one) of these hypothesis can and will be true.
To prove our research hypothesis, we hence have to have sufficient evidence to reject the null hypothesis. In our example, we need enough evidence to reject the null hypothesis that the average height of males in Germany and the US is the same. Our goal hence is to collect some data and see which hypothesis will be supported.
Let’s say you randomly choose 5 American and 5 German males and record their heights.
Sample of Germans: 69 in, 74 in, 70 in, 69 in, 71 in
Sample of Americans: 68 in, 73 in, 70 in, 69 in, 72 in
The average height of Germans in your sample thus is 70.6 inches, while Americans on average are 70.4 inches. We see that these two averages are not exactly equal – but they are close! But does this small difference really prove our research hypothesis? Is this data statistically significant? Keep in mind, we only polled 5 individuals from either country. If we had randomly chosen 10 different people, would we be drawing a different conclusion?
How sure do we want to be that we are not making a mistake?
Since it is practically not feasible to calculate the average height of all German and all American males, there is always a small risk that your conclusion, based on your samples, will be incorrect. The average height of German and American males may truly be the same, but based on our sample, we may conclude they are not. When we erroneously reject the null hypothesis even though it is true, that’s what we will call the “Type 1” error. On the other hand, if we do not reject the null hypothesis even though it is false, we make a “Type 2” error.
Remember that our goal is to be confident that the null hypothesis is not true, so that we can reject it and accept the alternative, which happens to be our research hypothesis. In other words, we want to be sufficiently sure that we are not making a Type 1 error. By convention, we will accept up to a 5% chance of accepting our research hypothesis even though it is not true. That’s what we also call the “significance level”.
As the bell-shaped curve below shows, if there is truly no difference between the means, then we’d expect the difference between the means that we find in our samples to be relatively close to 0. Only rarely would we expect to see a sizeable difference.
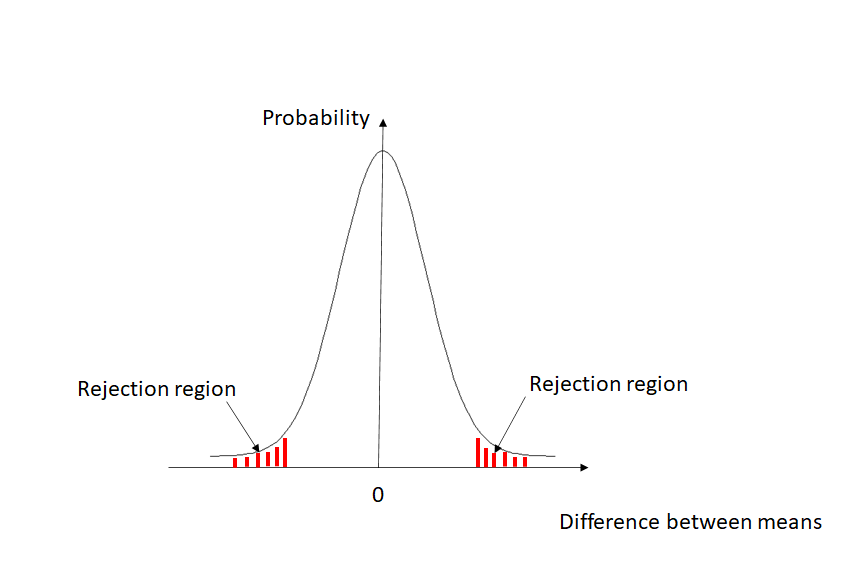
Testing our hypothesis
As we said before, we want to make sure that we only wrongfully reject our null hypothesis with a probability of up to 5%. The areas shaded in red in the graph above contain a total of 5% probability, 2.5% on either side. Hence, if the difference between our two average heights falls into either one of the regions shaded in red in the graph, we will feel confident enough that the two means in the samples are not the same and reject the null hypothesis that they are equal.
In our example, if we do what is called a two-tailed t-test for equal means of independent samples, we see that our difference does not fall into the rejection region. More specifically, if the two means are truly the same, there is an 88% chance to observe the small difference of 0.2 inches that we found in our samples. Intuitively, that is not too surprising since our sample size was rather small. With only 5 individuals in each group, a difference of 0.2 inches between the averages could very well be due to chance. In fact, in a small sample like this we are going to need to observe a difference of roughly 1.5 inches to call it statistically significant.
Practical vs. statistically significancant
As our example illustrates, whether differences are statistically significant depends on the sample size. In smaller samples, the difference we observe will need to be larger. In large samples, even small differences can be significant. This has important practical implications. For example, consider a new drug that claims to shorten the duration of symptoms of a disease. Suppose a study with 20,000 participants finds a statistically significant effect of half a day. While statistically significant in a large sample, this effect is likely not of practical significance. On the other hand, imagine another study with only 20 participants for a different drug finds a difference of 5 days. Since the sample was small, this turns out not to be statistically significant. However, this difference may be of practical significance. Statistical significance therefore does not necessarily equal practical significance of results.

As usual, the answer is “It depends.”
As you have seen, deciding whether something is statistically significant is not as straightforward as measuring the magnitude of the difference. If you are interested in learning more about hypothesis testing and how to analyze data, become a Buff and take courses in statistics, quantitative analysis or data analytics!
Anne-Christine Barthel
Assistant Professor of Economics and Decision Management


