After a long day of work, you decide to stop off at your favorite pub for a peaceful respite, only to find a tremendous pool tournament just getting underway. As you push through the crowd to the bar, you notice that the participants strike you as rather odd. Rather than the cool, confident, outgoing individuals you’re used to, this bunch appears to be rather geeky, aloof, and shy.
Here’s To Ya
“A faculty gathering?”, you ask yourself. “No, couldn’t be,” you conclude, as you take the first sip of your beer. But as you look closer, you find something truly astonishing: Instead of approaching the table with the normal sort of flippant swagger you’d expect, you find the players pouring over trigonometric calculations and classical mechanics textbooks in order to formulate the best strategy for their next shot.
“What kind of tournament is this?” you ask the bartender. “Oh, this is no tournament,” he replies, “These folks are economists, and they’re simulating a tournament. In fact, yours is the first beer I’ve sold all evening.” He heads to the back, shaking his head.
The situation I’ve just described is an elaboration on one of the most famous analogies in modern economics, made popular by Nobel Prize winning Milton Friedman himself. The current paradigm among economists is to use an assumption known as “rationality” as a starting point for modeling the behavior of economic agents, including consumers, business owners, and policy makers.
Everybody Into The Pool
This economic notion of rationality, which is quite distinct from the everyday use of the word to describe reasonable or sane behavior, results in a precise mathematical method for formulating the “optimal” decisions of economic agents.
For example, an economist would assume that rather than relying on the rule-of-thumb heuristics and intuition that an actual pool player has accumulated over years of practice, their shots are guided by the precise laws of geometry and calculus, and by the perfect foresight of what their opponents will do during their next shot. As a more direct economic example, business managers are assumed to make perfect cost/benefit decisions in order to maximize the profit for their company.
The name “Homo Economicus” has been given to such fictional god-like rational calculators.
However, the drawbacks of such an approach seem obvious. Surely pool players and business managers aren’t able to solve complex mathematical equations in their head in the blink of an eye. To this line of criticism, Milton Friedman offers a famous response:
“It seems not at all unreasonable that excellent predictions would be yielded by the hypothesis that the billiard player made his shots as if he knew the complicated mathematical formulas… Our confidence in this hypothesis is not based on the belief that billiard players, even expert ones, can or do go through the process described; it derives rather from the belief that, unless in some way or other they were capable of reaching essentially the same result, they would not in fact be expert billiard players.”
– Milton Friedman, Essays in Positive Economics, 1953
Dive Into The Literature
In other words, although pool players (or business owners) may not actually be solving equations in their heads, they will, over time and with experience, eventually behave as if they are.
This article is my attempt to gauge the strength of Milton’s response through the lens of my personal experience and reading of the literature. To that end, I believe a rough first pass can be made by comparing actual economic outcomes with their theoretical predictions along two lines.
The first concerns the amount of agents who are interacting in a given economic situation. For example, are we talking about an entire macroeconomy filled with millions of buyers and sellers, or two drivers who happened to pull up at a stop sign at exactly the same time?
The second concerns the amount of time that agents have to learn their environment. That is to say, do agents find themselves in an economic situation in which they can learn from past mistakes, such as the stock market, or are we considering a situation in which they must make a single one-off decision, such as buying a house?
Dividing up the battlefield in this manner, I will describe two scenarios in which I believe Milton’s response holds up remarkably well, and present a third in which economists still have work to do.
Case 1: A Large Amount of Agents
As an undergraduate at the University of Central Florida, I had the pleasure of attending a lecture by one of the leading experimental economists, Charles Plott. I also had the pleasure of attending a talk by the Nobel Prize experimental economist Vernon Smith as a graduate student at the University of Kansas. Both of these individuals have dedicated their careers to investigating whether real-life outcomes match the predictions made by economic theory, primarily in market settings where there are a lot of agents present.
The general consensus of such investigations reflects very positively for the field of economics. In his seminal paper “An Experimental Study of Competitive Market Behavior”, Smith sets out to test the hypotheses of neoclassical market theory, and finds a strong tendency for theoretical predictions to reflect actual market behavior.
Plott et al., also found very positive results in a 2017 study of call markets. In a very interesting multinational study in which individuals from Israel, Japan, the United States, and Yugoslavia participated in a simulated market scenario, Roth et al. found that experimental outcomes all converged to the correct theoretical predictions.
Although there is an entire literature on market experiments in various settings, my general reading is that such positive results tend to be the norm. One might expect that with a large amount of market participants, errors in judgment tends to “average out,” so that behavior pretty accurately reflects the correct theoretical predictions in the aggregate. As the above results indicate, this generally seems to be correct.
Score one for Homo Economicus.
Case 2: Long Time Horizons
I am going to do a bit of shameless advertising on this one. In the paper “Coordination and Learning in Games with Strategic Complements and Substitutes”, co-authors Anne Barthel, Andrew Monaco, and I set out to study whether or not experimental participants eventually come to behave in a way that is consistent with the theoretically predicted Nash equilibrium if given enough time to adjust and learn from past mistakes.
We studied this hypothesis in four different types of games, called “GSC High”, “GSC Low”, “GSS High”, and “GSS Low” (the reason for these names is not important here), and allowed participants to play these games over 20 rounds each. The graph below summarizes our findings:
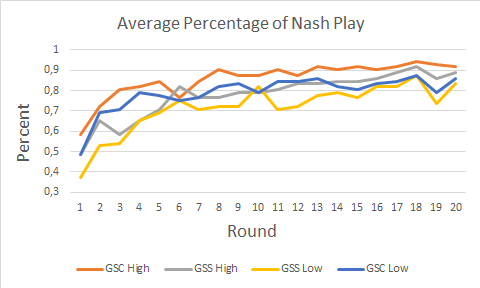
As is evident from the graph, in the early rounds of the game, the results are not so promising: While participants in the “GSC High” game behaved according to the theoretical prediction roughly 60% of the time, participants in the “GSS Low” game did so only around 35% of the time. However, after enough rounds, participants became acquainted with the environment and were able to learn from past mistakes, and the theoretical outcomes begin to show remarkable predictive power.
GSS Low, still the worst performer, nevertheless exhibited equilibrium play around 85% of the time, where GSC High was over 90%. Although unverified, one may conclude from the upward trajectory in the graph that even more rounds of play would result in almost perfect convergence to equilibrium.
These results are very typical of situations in which individuals have the opportunity to learn from their past mistakes and try again. For a more comprehensive overview of such experiments, I refer the interested reader to a great overview of similar studies in Colin Camerer’s “Behavioral Game Theory: Experiments in Strategic Interaction”.
In the meantime, score two for Homo Economicus.
Case 3: Few Agents, Short Time Horizons
In scenarios in which there is a very small amount of individuals who do not have sufficient time to learn from past mistakes, the picture is mixed at best. Indeed, revisiting the figure used in Case 2 above, we see instances of situations in which individuals behave according to theory significantly less than half of the time.
Unfortunately, failures of this magnitude are not hard to find in the experimental literature. In fact, during a study in which Holt, et al., studied behavior in a game called the “Prisoner’s Dillema.” You can learn more about if you take my ECON 4301 course, the conclusion is grim: “And yet, among the more robust findings to come out of experimental economics is that human players do not behave as game theory predicts” they write, in the context of this class of experiments.
If we’re being fair, Homo Economicus is the loser here. However, where there is failure, there is opportunity. Since the realization that requiring real human beings to make complex calculations in one-off scenarios can sometimes be too much to ask, concepts such as bounded rationality, self-confirming equilibria, quantile response equilibria, k-level reasoning, and a host of others have popped up in order to try to fill the gap.
While many of these approaches have proven to be very successful, some tend to work better than others depending on the nature of the situation, and a “general approach” still eludes us. In other words, there is still a lot of exciting work to do in economics.
Conclusion
My view is that Friedman’s response has generally proven to be the right way to think about things. Given enough time to learn, or in the presence of enough agents so that mistakes “average out,” theory tends to predict very well. Yes, cases in which predictions aren’t fulfilled in experiments with long time horizons or many agents can be found. But cases with short time horizons and few agents in which theory predicts wonderfully can be found as well.
At bottom, though, it seems that theory holds up to evidence pretty well in most of the settings economists are interested in, including general market outcomes and dynamic competition between firms, and I am therefore of the mind that whatever approach eventually reigns supreme, it will have to subsume the traditional concepts of market and Nash equilibrium that we use today. The data simply shows it.
Eric Hoffmann
Assistant and Pickens Professor of Economics
References
- Barthel, Anne-Christine, Eric Hoffmann, and Andrew Monaco. “Coordination and learning in games with strategic substitutes and complements.” Research in Economics 73.1 (2019): 53-65.
- Friedman, Milton, and Marilyn Friedman. Essays in positive economics. University of Chicago press, 1953.
- Holt, Charles, Cathleen Johnson, and David J. Schmidtz. “Prisoner’s Dilemma experiments.” The Prisoner’s Dilemma. Cambridge University Press, 2015. 243-264.
- Plott, Charles R., and Kirill Pogorelskiy. “Call market experiments: Efficiency and price discovery through multiple calls and emergent Newton adjustments.” American Economic Journal: Microeconomics 9.4 (2017): 1-41.
- Roth, Alvin E., et al. “Bargaining and market behavior in Jerusalem, Ljubljana, Pittsburgh, and Tokyo: An experimental study.” The American economic review (1991): 1068-1095.
- Smith, Vernon L. “An experimental study of competitive market behavior.” Journal of political economy 70.2 (1962): 111-137.


