Why Ponzi Schemes Fail: A Lesson in Exponential Growth

We’ve all heard of them. Ponzi schemes. From Bernie Madoff, to that one “entrepreneurial” friend who is always asking you to join his business. But what are they exactly, and why do they usually wind up being a disaster?

According to Investopedia, “A Ponzi scheme is a fraudulent investing scam which generates returns for earlier investors with money taken from later investors.”Aside from being illegal, I hope to show in this article why the math is stacked against such a business model having long-term success.

As the definition above suggests, a Ponzi scheme is a situation in which early members get paid by means of new members joining and putting their money into the company. These new members are then promised to be paid their investment with some interest because of even newer members joining in the future. Often, this “pyramid” structure is cleverly hidden within the fine details of the business, so that investors aren’t even aware that they are participants in such a scheme.

Visualize This

It will help us to visualize this structure for the purpose of our discussion. Suppose for simplicity that for every investor, there needs to be two more investors in order to both pay back the original investor with some interest, as well as allow the company to take a little bit of profit off the top. If we call the former Investor 1, and the latter Investors 2 and 3, then we get the following representation:

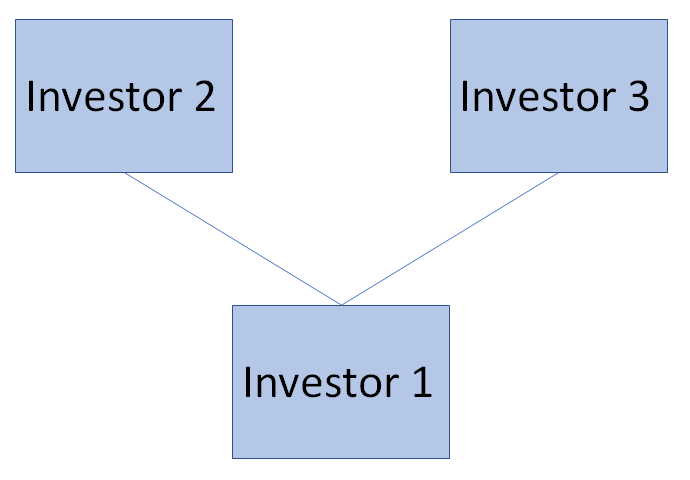
So far, so good. But notice that Investor 2 and Investor 3 will each need two more investors to maintain the scheme. And those investors will need two each as well. If we continue in this manner, we begin to get a picture that looks like this, where the arrows indicate that this process continues indefinitely:

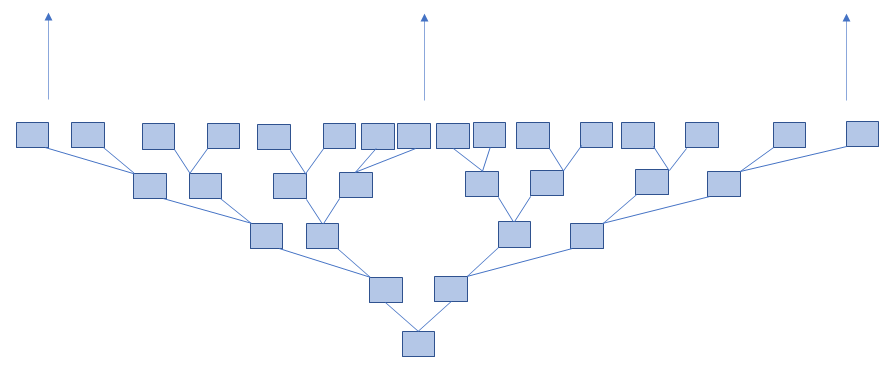
Exponential Growth

We see that the amount of participants must get really large, really fast if the entire scheme hopes to sustain itself. What I want to do is take a closer look at exactly how fast such an organization has to grow.

Let’s ask the following question: Given that there are a certain number N of individuals in our Ponzi scheme today, how many more members do we have to add in the future? Well, each of the N members will require 2 more members to be added, and hence we will need to add 2N extra members in order to keep our scheme going.

So let’s back up and start this from the beginning. On the first day, there are 2⁰=1 members. Then, by our above logic, we will subsequently need to add 2×2⁰=2¹, or 2 more members. Then, on top of that, we will have to add 2×2¹=2², or 4 more members. We are starting to see a pattern emerge. If we continue out this logic, then in time period x, we will need to add 2^x more members in order to keep the Ponzi scheme going.

Sheer Trickery

After a little bit of mathematical trickery, which you’ll learn plenty of in my CIDM 6305 class, we see that the equation y=2^x is exactly equal to the equation

                                                                                          y=e^ln(2)x

which is nothing more than an example of an exponential function. The thing about exponential functions is that they grow very rapidly. We can see this by plotting this graphically, where the x-axis is the time period, and the y-axis is the amount of new members we have to add in order to keep the Ponzi scheme going:

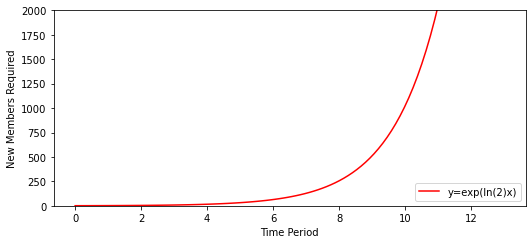
Notice that even in time period 8, we are already in a position where we need to add 256 new members in the next period. By time period 12, we need to add 4,096! This quickly becomes unsustainable.

The Cookie Crumbles

How could a Ponzi scheme manager overcome this fact? One thing they may try is to figure our a way so that instead of needing 2 new people for each 1 member, they may only need, say, 1.25 new people. Or maybe 1.1. Heck, maybe they get really clever and only require 1.05. Does this help matters? Only temporarily. If we do the same exercise as above with each of these three numbers, we end up with equations    y=e^ln(1.5)x,    y=e^ln(1.1)x, and    y=e^ln(1.05)x, respectively. Unfortunately for the Ponzi schemer, these are still exponential functions. Graphing these gives us the following:

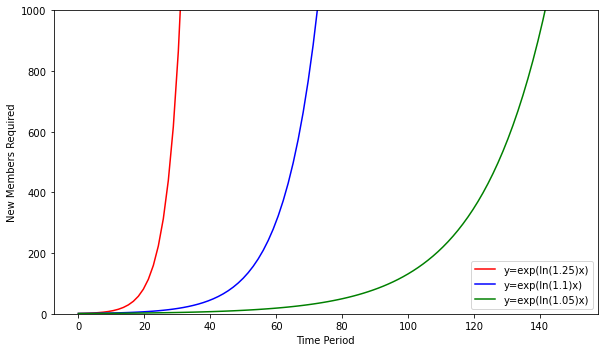
We see a general rule here. If each period the Ponzi scheme requires “b” new members in the next period for each one member in this period, they will require a total of y=e^ln(b)x new members each period. Anyway you slice it, it will be exponential, and maintaining such explosive growth is impossible for even the best of companies. Eventually, this required growth will not be sustained, people will begin not to get paid, and the Ponzi pyramid will crumble.

References

https://www.investopedia.com/terms/p/ponzischeme.asp