“Bitcoin’s exponential growth cools”, “Measles cases show signs of exponential growth in western Canada” and “Smart Buildings to see exponential growth in IoT devices by 2030” – these are just a couple of examples for news headlines that mention a concept that most of us encountered in a math class in school a long time ago: exponential growth. Most people probably equate it in their minds with “fast growth”. But what is exponential growth really? And more importantly, what does it mean for us?
Back to school
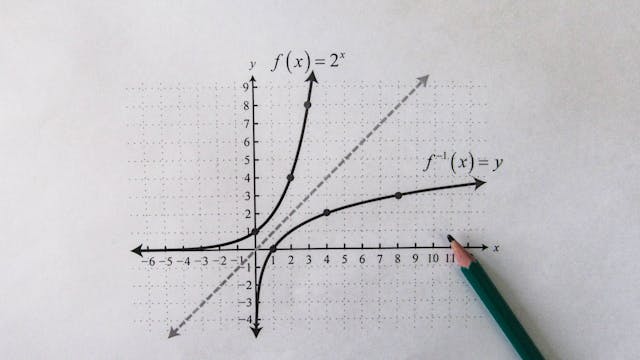
So, what is exponential growth? One simple definition says that exponential growth means that something grows as an exponential function of time. What this means intuitively is that something grows at a rate that is proportional to its current size. To apply this concept to one of the headlines from above, if we have twice as many active cases of a disease that spreads exponentially, new cases will be growing twice as fast as they are now.
Another way of visualizing the idea of exponential growth is the story of the lily pad pond. Picture a pond with only one lily pad in it. Every month, the number of lily pads doubles. Thus, in month 1, we have one lily pad, in month 2 we have 2, in month 3 we have 4, and so on. The “riddle” then usually asks something along the lines of “If we know the pond will be fully covered after 36 months, when will be half covered?”. Given that the coverage doubles every month the answer must be 35 months (even though our linearly thinking brains might be tempted to answer 18 – supposedly that’s why this is a popular interview question).

Throwback to 2020
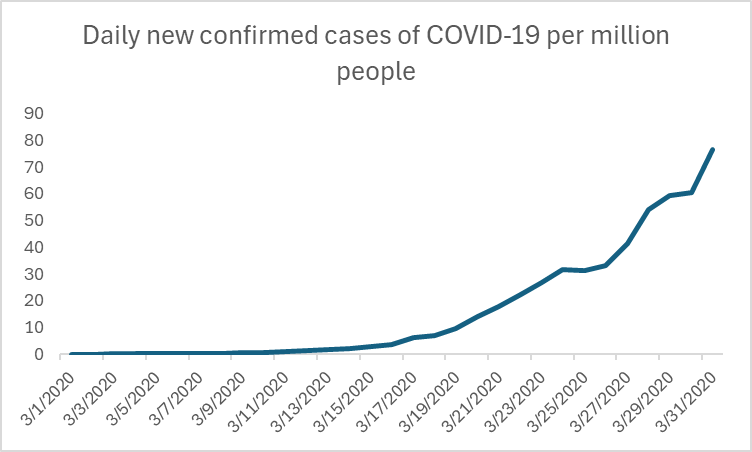
I think all of us heard and read a lot about exponential growth at the beginning of the Covid-19 pandemic. If we look back at newly confirmed Covid-19 cases in the United States during the month of March of 2020 and plot the data over time, we get the following graph.
Population based on various sources (2024)
– with major processing by Our World in Data
In this data, we see the same exponential growth pattern as with the lily pads – initially, the number of total cases climbs slowly, but the more cases we have, the quicker the number of new cases grows. In this case, exponential growth does not work in our favor (assuming that none of us like to be sick). Hence, we all witnessed worldwide attempts to “flatten the curve” through various measures such as lock-downs and masks to curb the exponential growth of new cases.
The power of compound interest
Luckily for us though, there are also plenty of examples of when exponential growth works to our advantage. One of them is the power of compound interest. When we invest or save money and earn interest on it, then each period we don’t only earn interest on the initial amount that we invested, but also the previously earned interest. What this means for us is that investing and saving as much as we can early in life will pay big dividends later.
Suppose a young adult has $1000 of savings for an initial deposit. Instead of spending the money, they invest it in an index fund. The average return of the S&P 500 over the last 30 years has been around 9%, but to be conservative let’s assume this person will on average get a 6% return on their investment.
In the table below, I have calculated the total final balance of the investment account for varying monthly contributions ($100, $500 and $1000) over the course of 35, 40 or 45 years. I used this online compound interest calculator, assuming monthly compounding.
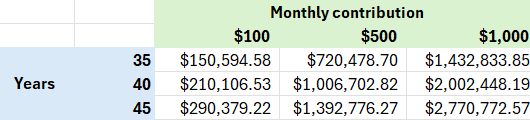
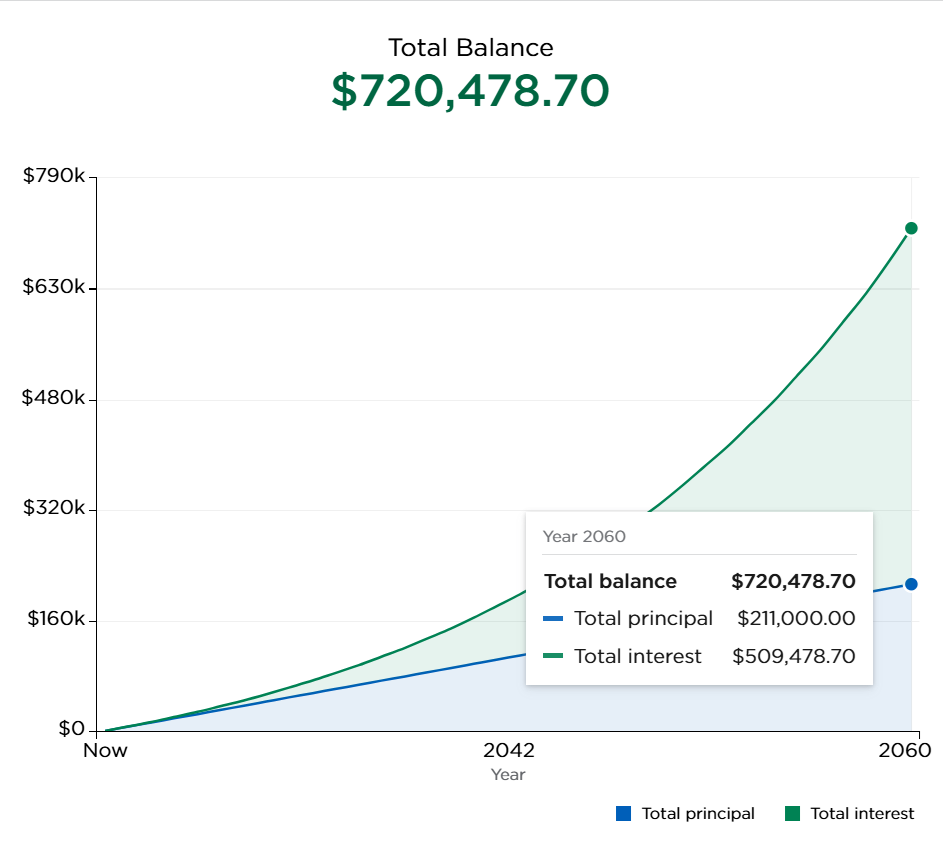
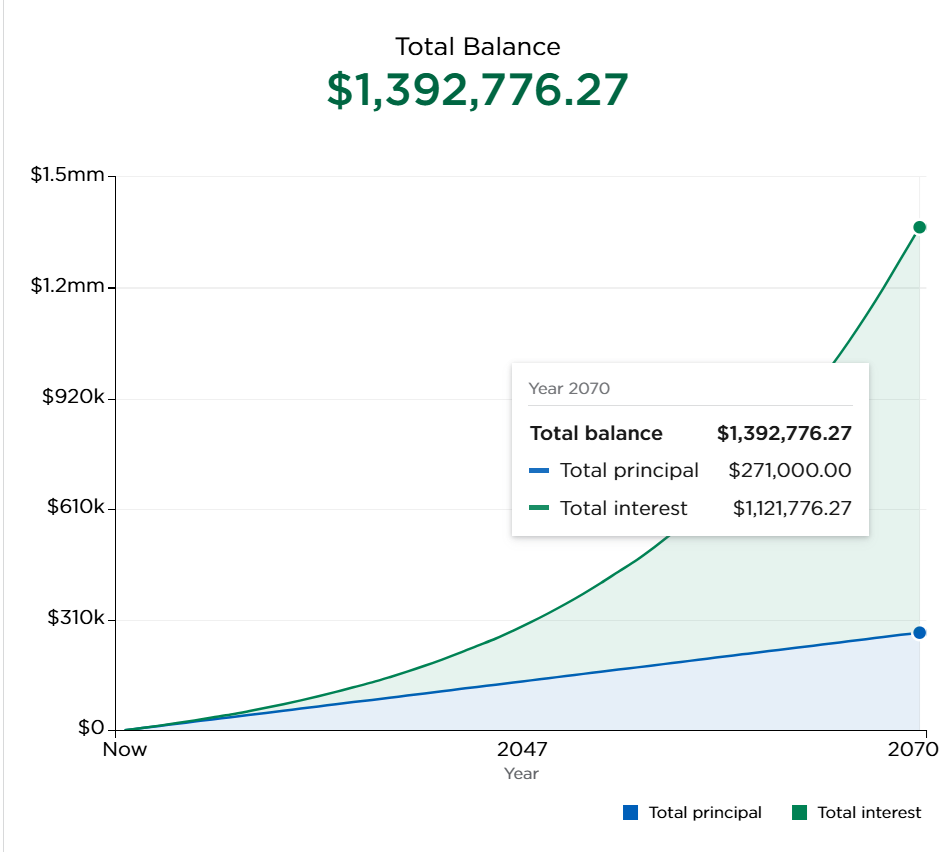
What we can learn from this are two things: Investing early matters and investing more on a monthly basis matters. First off, those who invest more on a monthly basis will end up with more at the end, which we see as we compare the total amounts within each row. If we compare along columns, we see that an individual that invests for an additional 10 years (45 instead of 35 years of investment growth) ends up with almost twice as much money. If we think of the years of investment growth as the working life of an individual, starting to save for retirement at 20 vs 30 years of age makes a big difference if we hold contributions constant.
The two figures below show how compound interest drives the stark difference in final account balance. I have plotted the account total growth for a $500 monthly contribution for 35 years (on the left) and 45 years (on the right). We see that the total principal (the money that the individual paid in) only differs by $60,000 – the rest of the difference is driven by the additional interest!
Math is all around us
While exponential growth may not always be intuitive for us, we are surrounded by many processes in the world around us that are evolving in that manner. The more we understand the dynamics behind them, the better we can leverage them to achieve our goals like saving for retirement or controlling the spread of infectious diseases. If you enjoy thinking and learning about how mathematical concepts shape the business world around us, become a Buff and take courses in economics and finance!