Imagine walking from one side of a room to another. Suppose it’s 2 meters long. Simple enough. You take a step. You take another. Before you know it, you’re halfway across the room. As you continue walking, you eventually find yourself having covered half of the originally remaining distance, and then half of that remaining distance, and so on.
Now if we’re being totally logical about this, then at every point in time, you are always on your way to covering half of some remaining distance. And if we carry this logic out to its conclusion, then at no point in time should you ever reach the end of the room.
The above riddle is known as Zeno’s paradox, first formalized by Greek philosopher Zeno of Elea in order to develop the claim that motion is no more than an illusion. Now, Zeno was certainly no fool. He knew it was more than possible to travel from one end of a room to the other. Logic, of course, is our guiding light as to what is true about the world (as many ancient Greeks were keen to stress). And motion just doesn’t happen to fit nicely into this framework. Our intuitive idea of motion is the unfortunate odd man out and must be the one to go.
Solution, Please
Surprisingly, philosophers to this day still wrestle over what the most reasonable solution to this paradox is. Physicists don’t lose any sleep over it. Mathematicians, on the other hand, have had a handy solution to this problem. This dates to Euclid, who wrote his famous Elements of Geometry about 700 years after Zeno’s time.
To get a sense of this solution, which is now known as a “geometric sum,” consider our example from above. We walk halfway across a 2 meter long room, or a total of 1 meter. Then we walk another half of the remaining distance, or another ½ of a meter. Then we walk another half of that remaining distance, and so on. If we write out all of these distances, we get
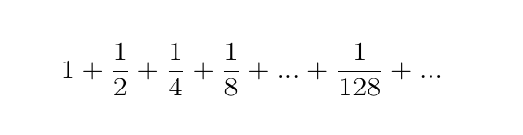
To Sum Up Zeno’s Paradox
If we really want to get fancy with it, then because the number 1 is nothing more than (1/2)0 , and 1/2 is nothing more than (1/2)1, and 1/4 is nothing more than (1/2)2, and so on, then this entire sum of distances can be put into “summation notation” and expressed as
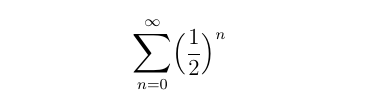
Now, it turns out that there’s a fancy trick to figuring out what this sum must come to, which was Euclid’s insight. The proof of this goes beyond the scope of this article, but in general, if z is any number between 0 and 1, then such a sum is equal to
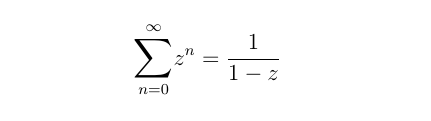
Ok, that’s cool, but what does this have to do with Zeno’s paradox? Well, let’s see what happens when we plug in z = ½ , just as we formulated our problem above:
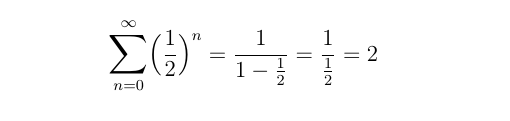
What this tells us is that if we do walk these half-distances forever and ever, then we will eventually walk the full 2 meters! Had ol’ Zeno been aware of how to add up all of these numbers, his paradox would not have been a paradox.
Now this is quite a nifty solution. It turns out that this also has a very interesting application to economics, which has recently come to my attention via a brilliant insight of a former student of mine.
The Government Multiplier
One of the joys of teaching for me is that every now and then, a student will point something out to me. This allows me to see some of the material I’ve been teaching for years in a new light. This happened a few semesters ago in my Econ 3312, Intermediate Macroeconomic Theory course. The topic was the government multiplier, which is the idea that government spending has a “ripple effect” in the economy.
For example, if the government spends $100 on a specific project, then that money will go into the hands of the employees associated with that project. They will then take that earned money and spend a fraction of it on private goods. Those sellers will take that money and further spend a fraction of it, etc. Furthermore, if the government project is effective, it itself will spur further economic activity. Examples include when a road or other infrastructure is built or improved. This multiplier is often expressed as the number
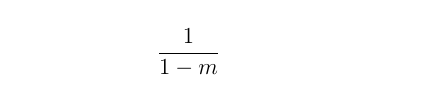
where m is a number between 0 and 1, known as the “marginal propensity to consume.” The marginal propensity to consume is simply that fraction of newly acquired income that you would choose to spend on consumption rather than save. For example, if m=.25, this suggests that you would spend 25 cents of every extra dollar earned on consumption. And if this happens to be the marginal propensity to consume in the economy, the government multiplier turns out to:
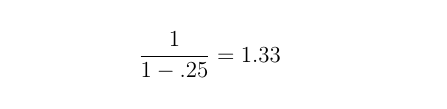
This tells us that every dollar spent in the economy through government spending is essentially equivalent to $1.33 over time.
But Wait, There’s More
This is where things get interesting. Notice that our multiplier equation bears an interesting resemblance to our geometric sum equation, but with an “m” instead of a “z”. Is there a connection between these two concepts? It had never struck me that there was, but then a brilliant student of mine named Richard Jones asked a question in class. “Dr. Hoffmann, is that government multiplier term basically just the total sum of money that eventually exchanges hands over time?”
A light bulb went off in my head. This is exactly what this was, and this was nothing more than our old friend, the geometric sum.
At The Margin
You see, if m is the marginal propensity to consume, which we can assume to be .25 as an example, this is simply saying that .25 of every dollar you earn will go towards further consumption. Then if the government stimulates the economy by $1, this itself becomes income for some individual who will subsequently spend .25 of that towards further consumption. But the individual receiving that money will spend .25 of that, or (.25) x (.25)= (.25)2 of the original dollar. And then .25 of that, which is a total of (.25)3 of the original dollar, gets spent again, and so on. If we keep track of all of these payments, we get:
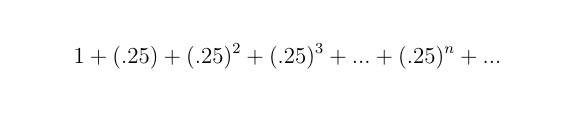
This is nothing more than our geometric sum above with z set equal to the marginal propensity to consume! Therefore, for any marginal propensity to consume m that we’re interested in, the “total sum of money that eventually exchanges hands over time”, as Richard would put it, is exactly:
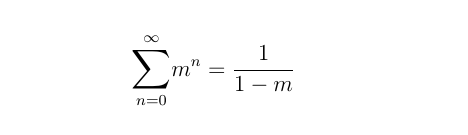
As we know, this is nothing more than the government multiplier from above. Interestingly, if you were to derive the government multiplier in class, you would arrive at the same term but through a much different motivation and methodology. But that these two approaches line up to tell the same story from different angles is just a little insight that I thought was worth writing down. I’ll forever be grateful to Richard Jones for helping me to see this.
Dr. Eric Hoffman
Associate & Pickens Professor of Economics


